Price Elasticity of Demand (PED) Explained with Graphs

The price elasticity of demand relates to a product (a good or service) and its demand sensitivity to changes in its price. In other words, it measures the amount by which consumers will adjust how much of the product they will want to purchase as its price increases or decreases.

We know from the first law of demand that, at higher prices, consumers will demand a lower quantity of a normal good (and vice versa for lower prices). But the price elasticity of demand goes further than this and calculates the extent of those movements in demand.

For some products, a change in price brings a larger change in demand than it does for others, and this should be intuitively obvious with a little thought. If the price of basic necessities increases, our demand for these products is more or less unchanged because we have to have them. Other goods are more dispensable, and so our demand for them is more sensitive to price changes.

Time is another consideration when thinking about the price elasticity of demand for a product, because we may be able to react to some changes over the long-term that we can’t really do much about in the short-term, or vice-versa.

What are the Determinants of Price Elasticity of Demand?

There are several factors that influence the price elasticity of demand for a product:

• Availability of Substitutes: If there are many substitutes, demand is more elastic since consumers can easily switch to another product.
• Necessity vs. Luxury: Necessities tend to have inelastic demand, whereas luxury goods are more dispensable and therefore more elastic.
• Time Period: Demand usually becomes more elastic over time as consumers find alternatives, or adjust their spending habits.
• Durable Goods: For durable goods, like washing machines, demand is more elastic in the short-run as consumers react to price rises by making do with what they have - but eventually they will buy.
• Proportion of Income Spent: Goods that take up a significant portion of consumers’ income, like cars and houses, tend to have more elastic demand.
• Addictiveness: Products that are addictive, such as tobacco and alcohol, usually have a relatively inelastic demand.

Can Elasticity of Demand be Negative?

Yes, in fact it is always negative for normal goods since any increase in price always leads to a decrease in quantity demanded. There are some exceptions, but these apply to different types of economic goods i.e. Giffen Goods and Veblen goods, where demand actually increases as price increases.

Price Elasticity of Demand Graph

In the graph below I have illustrated a typical demand curve for a product. It is downward sloping indicating the inverse relationship between price and quantity. It displays one portion of the curve that has inelastic demand, and another that has elastic demand. Inelastic demand occurs at quantities below 25, and elastic demand occurs at quantities above 25.

Inelasticity at lower quantities relates to the relative scarcity that occurs at lower amounts, and increased reluctance to give up more of the product. In this sense, as the slope of the demand curve gets steeper, demand becomes more inelastic. However, slope alone is insufficient to determine elasticity, for that we need to consider total expenditure (see below).

Price Elasticity of Demand Formula

The price elasticity of demand is defined as the percentage change in quantity demanded divided by the percentage change in price. The formula for this is:

PED = %ΔQ / %ΔP

The triangle Δ is used to denote ‘change’. Depending on the value of PED, demand for a product can be classified into different categories:

• Elastic Demand (PED > 1): A small change in price leads to a larger change in quantity demanded. This is common for luxury goods, electronics, and restaurant meals, where consumers are sensitive to price changes.
• Inelastic Demand (PED < 1): Demand is less responsive to price changes. Essential goods like salt, water, and gasoline typically fall under this category, as consumers continue to purchase them despite price fluctuations.
• Unitary Elastic Demand (PED = 1): The percentage change in price results in an equal percentage change in demand.
• Perfectly Elastic Demand (PED = ∞): Any price increase leads to zero demand, often seen in perfectly competitive markets with identical substitutes.
• Perfectly Inelastic Demand (PED = 0): Demand remains constant regardless of price changes, as seen with life-saving medications like insulin.

Another, simpler method, that defines elasticity is given by what happens to total expenditure as the price of a product changes. Table 1 below categorizes these movements, but it fails to give a specific value (or coefficient) that measures the extent of elasticity or inelasticity. I’ll show how to calculate the price elasticity of demand coefficient in a section below.

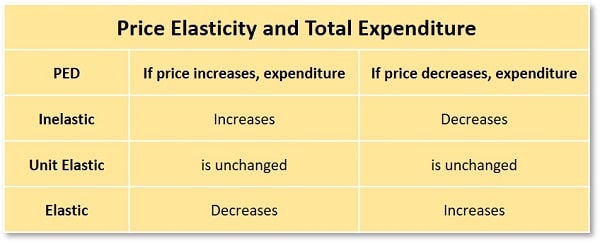Table 1

Isoelastic Demand Graph & Unitary Elasticity

The Isoelastic demand graph illustrates a curve with unit elastic demand i.e., where any change in price is matched by an equal offsetting change in quantity demanded, such that total expenditure is unchanged.

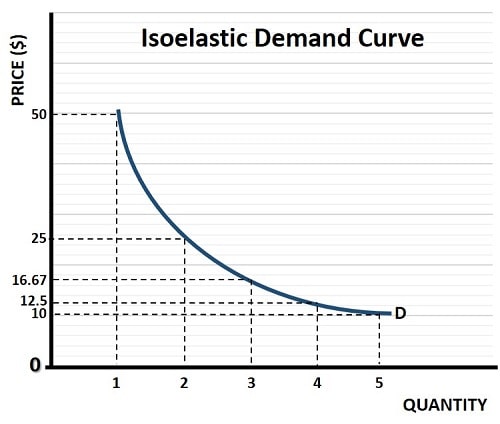
Unit elasticity of demand is, of course, more of a theoretical concept rather than a common occurrence in the real world. However, it does help us to think about elasticity in a more robust way.

As mentioned above, it is not the case that elasticity depends on slope alone, we also have to consider how expenditure changes. We can have a demand curve that is price elastic along its entire curve, and we can have a demand curve that is inelastic along its entire curve, or even unit elastic as in the graph above.

Perfectly Inelastic Demand & Perfectly Elastic Demand Graphs

As can be seen on the left-side of the graph below, perfectly inelastic demand means that any change in price at all has no effect on the quantity demanded i.e. consumers regard it as an essential item. Since the change in quantity is zero, dividing that by any price change is also zero, meaning that perfectly inelastic demand has a coefficient of zero.

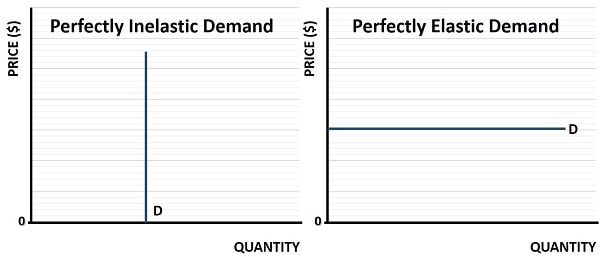
On the right-side of the graph above, perfectly elastic demand means that any increase in the prevailing price will be met with a total loss of demand. This means that, with a zero change in price, the quantity change divided by zero gives an infinite elasticity coefficient.

How do you Calculate Price Elasticity of Demand?

There are two standard approaches to calculating the price elasticity of demand depending on whether we are looking at a particular point on the relevant demand curve, or over a range of that curve.

Point elasticity of demand is illustrated on the left-side of the graph below. I’ve shown two different points on the demand curve for a given product. At point A demand is relatively more inelastic than at point B (we can see this due to the steeper slope of the curve at that point). We cannot calculate the point elasticity without an equation that defines the demand curve but, if we had that equation, we could use a technique in calculus called differentiation to work it out.

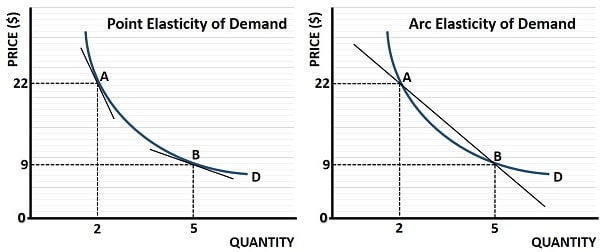
On the right-side of the graph above I have again illustrated the same two points, A and B, and I have drawn a single line that passes through those points. We can use a method called the ‘arc elasticity of demand’ (also known as the midpoint formula) to give a single measure of elasticity between these two points. We do this with the following formula:

ARC PED = (ΔQ/ΔP) (P*/Q*)

P* and Q* are the average prices and quantities for points A and B.

This works out as:

(3/-$13)($15.50/3.5) or -.23*4.43 = -1.02

As is the convention, we ignore the negative sign and simply conclude that the arc elasticity of demand coefficient over this range is 1.02, which is slightly elastic. We can check this with table 1 above to see what happened with total expenditures.

At point A there was a total expenditure of $44 while at point B this rose slightly to $45. Table 1 shows that when price decreases (as it did from point A to point B) an increase in total expenditure indicates elastic demand.

The Elasticity of Demand Coefficient

The price elasticity of demand coefficient gives a simple number that economic agents can use to assess how responsive total expenditure is to price changes. This information has obvious value to producers who will want to estimate the demand for their goods and services at different price points, but it has other uses too, especially for government policy makers.

Price Elasticity of Demand Examples of Usage

PED plays a vital role in various economic and business decisions.

• Business Pricing Strategies: Companies analyze demand elasticity to set optimal prices and maximize revenue. If demand is inelastic, they can increase prices without losing a large number of sales.
• Government Taxation: Governments impose higher taxes on inelastic goods, like cigarettes and fuel, because demand remains stable despite price hikes. The extra taxes raised can then be used to fund the healthcare costs and pollution costs associated with these goods.
• Policy Decisions: Understanding PED helps policymakers regulate essential goods, ensuring affordability and market stability. It also gives vital information about the effects of raising tariffs on certain imported goods, in terms of estimating revenues raised and reductions in trade.

FAQs about Price Elasticity of Demand

Conclusion

Price Elasticity of Demand helps measure how sensitive consumer demand is to changes in price. Various factors influence elasticity, including the availability of substitutes, whether a good is a necessity or a luxury, the time frame considered, and how much of a consumer’s income is spent on the product.

PED can be classified into different types, from perfectly inelastic to perfectly elastic, and has many real-world applications in business pricing strategies, government taxation, and policy decisions.

Related Pages:

• Income Elasticity of Demand
• Cross Price Elasticity of Demand
• Consumer Behavior

ShareFacebookXPinterestTumblrRedditWhatsApp