The Marginal Rate of Technical Substitution (MRTS) in Economics

The marginal rate of technical substitution is an important component of the ‘theory of the firm’, and it focuses on how firms choose to allocate various inputs into the production process according to their relative marginal product.

As usual it is standard practice to restrict the model to just two inputs i.e., labor and capital. This is a huge simplification of any real-world scenario, but with only two inputs in the model we can use a two-dimensional graph to illustrate the important points under consideration without unnecessary complications.

The MRTS is a long-run model, meaning that firms have time to adjust both labor and capital as they wish, but all other long-term factors are held constant e.g., technological advances and shifts in market dynamics. Additionally, we assume that the firm is operating in a competitive market, and therefore input prices cannot be influenced by the firm’s input choices.

Diminishing Marginal Rate of Technical Substitution & Input Substitution

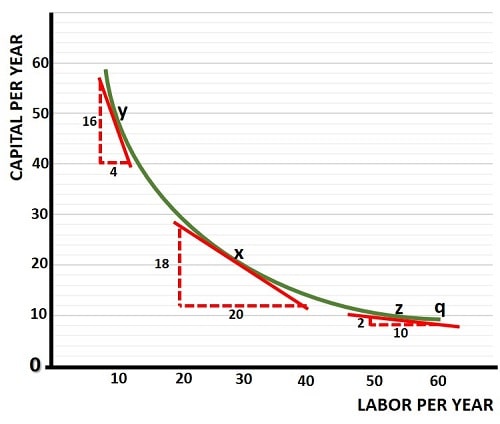
As illustrated in the graph above, there is a diminishing MRTS as we move down an isoquant curve from left to right. In words this means that, in order to decrease capital in the production process, we must substitute it with more and more labor if we wish to produce a constant level of output (and vice versa).

This is consistent with the law of diminishing returns.

Starting at point x in the graph above, to know what the MRTS of capital for labor is, we need to draw a tangential line that just touches the isoquant (q). Then, using the basic geometry of a triangle, we can determine the slope of the isoquant curve at that point. At point x, this is equal to 18/20 (or 0.9). The slope is downward, meaning that more of one input comes with less of the other, and therefore the slope is negative.

At point x, the marginal rate of technical substitution of capital for labor is equal to -0.9.

Using a similar process, we can see that the MRTS of capital for labor at points y and z are -4.0 and -0.2 respectively. In other words, there is a diminishing MRTS as we move along the curve.

I should point out here that the illustration here is used for simplicity. It’s much more likely that you will need to use calculus, i.e., differentiation of a given equation, to calculate the MRTS in an undergraduate level economics course.

The Marginal Rate of Technical Substitution Formula

Since the MRTS can be defined as the ratio of the marginal product of one input to the marginal product of another input, a model with two inputs (labor and capital) allows us to state that the marginal rate of technical substitution is equal to the marginal product of labor (MPL) divided by the marginal product of capital (MPK):

MRTS(LK) = MPL/MPK

In order to minimize the costs of production, a further condition must be that the MRTS is also equal to the ratio of wages (the cost of labor) and r (the cost of capital). This gives us this condition if output is to be produced efficiently with minimal costs:

MRTS(LK) = MPL/MPK = w/r

For more information on this, see my article about cost minimization for a firm.

What is the Difference between MRS and MRTS?

The Marginal Rate of Substitution (MRS) relates to a similar concept that concerns consumer preferences rather than the production process. When a consumer desires two alternative goods, the MRS is given by the amount of one good that a consumer is prepared to sacrifice in order to obtain an additional unit of the other good.

Clearly, the MRTS is more or less the same idea for producers, but it does not relate to any particular inherent desire for one input over another. Rather it relates to the desire to minimize overall costs, and thereby contribute towards profit maximization.

What is the Difference between MRT and MRTS?

The Marginal Rate of Transformation (MRT) is another similar concept in economics, but this refers to the rate at which a producer is willing to switch production from one good to another, rather than the rate at which inputs are substituted in order to minimize the costs of producing a given good.

The MRT relates to the Production Possibilities Curve, because increasing the production of one good necessarily means sacrificing production of another when productive efficiency is optimized.

Summary and Final Thoughts

The MRTS represents the amount by which the quantity of one input can be reduced when one additional unit of another input is used, and the level of output remains the same. It is used in production decisions and helps firms to optimize their input usage.

If the MRTS is constant, it implies that inputs are perfect substitutes. If it varies, it suggests that the inputs have a varying degree of substitutability.

While the concept is widely accepted in economic theory, there are a few points to keep in mind when using it:

• Assumptions of Perfect Competition - Critics argue that in real-world scenarios, where markets may not be perfectly competitive, the conditions under which MRTS is derived may not hold.
• Homogeneous Inputs - Inputs are assumed to be homogeneous, meaning that one unit of an input type is a perfect substitute for another. In reality, inputs may have different qualities or characteristics, making them imperfect substitutes.
• Static Nature - In dynamic and evolving industries, technological advancements, changes in factor prices, or shifts in consumer preferences can impact the relevance of MRTS as a long-term decision-making tool.

Related Pages:

• The Isocost Line
• Costs of Production
• The Production Function
• The Production Possibilities Curve

ShareFacebookXPinterestTumblrRedditWhatsApp