The Linear Demand Curve Explained (with a Graph)

A linear demand curve is a type of demand curve in economics where the relationship between price and quantity demanded can be represented by a straight line. In this case, the change in quantity demanded is constant for each unit change in price. The equation of a linear demand curve typically takes the form:

Qd = a − bP

Where:

• Qd is the quantity demanded,
• P is the price of the good or service,
• a is the intercept (the quantity demanded when price is zero),
• b is the slope of the demand curve (the change in quantity demanded for a one-unit change in price).

Characteristics of a Linear Demand Curve

Constant Slope: The demand curve has a constant slope, meaning that the relationship between price and quantity demanded is linear. For every unit increase or decrease in price, the quantity demanded changes by a constant amount.

Straight Line: The curve is a straight line, making it easy to graph and analyze. Consider the simple linear demand curve in the graph below. Demand here is defined by the equation: Q = 24 – 2P

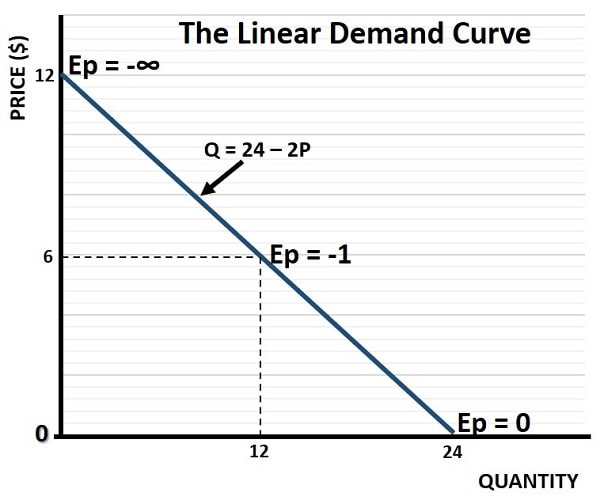
As can be seen, the price elasticity of demand (Ep) varies from negative infinity (-∞) to zero as the quantity demanded varies from zero to 24 (at which point price is zero). The elasticity value is always negative because the slope of the curve is negative i.e., there is an inverse relationship between price and quantity demanded, so that as one increases the other decreases.

At the top of the linear demand curve, elasticity is very high since a small decrease in price brings a proportionately large increase in quantity demanded. For the same reason, elasticity is smaller as the price approaches zero and quantity demanded approaches its maximum point.

The slope of the linear demand curve is a constant, and this is measured by calculating the change in quantity divided by the change in price. Mathematically this is expressed as:

Slope = ΔQ/ΔP

From the graph we can see that as quantity increases from 0 to 12, the price falls from $12 to $6. Therefore, the change in those variables is 12 and -6. The slope of this linear demand curve is then 12/-6 which is -2, and this slope is constant.

Why Economists Use Linear Demand Curves

Economists often use linear demand curves for several reasons, especially in simplified models or when introducing key concepts:

Simplicity and Mathematical Convenience

• Linear functions are easy to work with mathematically because they involve simple arithmetic and algebra. This makes it easier to analyze how changes in price affect demand.
• Linear equations have well-defined slopes and intercepts, which make it easy to calculate and interpret relationships between variables (e.g., price and quantity demanded).
• Linear demand curves give straightforward, predictable results for any given price.

Modeling Common Scenarios

• In many cases, linear demand curves serve as a good approximation for real-world markets, especially over a limited range of prices. Although actual demand curves might be non-linear, using a linear approximation can provide useful insights into consumer behavior in a specific price range.

Consistency in Economic Models

• Linear demand curves are often used in introductory economic models because they allow for clear, consistent teaching and understanding of economic principles (such as the law of demand, price elasticity, and market equilibrium).
• Using linear demand curves allows economists and students to focus on key concepts such as shifts in demand, elasticity, and the effects of price changes without the added complexity of non-linear curves.

Linear Demand and Supply for Market Equilibrium

• Linear demand curves, when combined with linear supply curves, make it relatively simple to find the market equilibrium (where the quantity demanded equals the quantity supplied). This is a foundational concept in economics.

Limitations of Linear Demand Curves

While linear demand curves are useful, they do have limitations. Real-world demand curves are often non-linear and the relationship between price and quantity demanded can change at different price levels. For example, at very high prices, a small change in price may cause a large change in quantity demanded, while at low prices, the opposite may happen. This is explained in my main article about the Demand Curve.

The slope of a linear demand curve implies that price elasticity is not constant. The elasticity of demand varies at different price points. In contrast, non-linear demand curves can more accurately represent variable elasticity across the range of prices.

Non-Linear Demand Curves

A non-linear demand curve does not follow a straight line. Instead, it may be curved, and the relationship between price and quantity demanded is not constant. Common forms of non-linear demand curves include:

• Exponential or Logarithmic Demand Curves – These curves may show diminishing or increasing responsiveness to price changes.
• Convex or Concave Curves – The demand may become more or less elastic as the price changes, indicating that consumers are more or less sensitive to price changes at different points.

Conclusion

Economists use linear demand curves because they are simple, mathematically convenient, and provide a clear understanding of the basic principles of demand, especially in introductory models. While non-linear demand curves might more accurately reflect real-world complexities, linear models are often a useful approximation and offer a straightforward way to analyze price-quantity relationships in a wide variety of situations.

FAQs related to the Linear Demand Curve

Related Pages:

• The Demand Curve
• The Inverse Demand Function & Curve
• The Compensated Demand Function
• Derived Demand
• Consumer Behavior

ShareFacebookXPinterestTumblrRedditWhatsApp