Constant Cost Industry Examples

At first glance, it might seem that a constant cost industry is nothing more than an abstract possibility, and quite removed from reality. This is because we are taught that supply curves are upward sloping and that any increase of output must come with higher costs and prices.

This is true, in most cases. However, the idea behind the constant cost industry is one of long-term adaptation. The supply curve that we are most familiar with is a short run supply curve that exists within a timeframe that does not allow firms to expand production by building new plant and equipment, and only by squeezing more production from existing facilities.

With a long-term horizon this restriction is lifted, and costs are determined by the inputs used to create new output i.e. land, labor, capital, and entrepreneurship. If these inputs are abundantly available then there is no obvious reason why output cannot be expanded with the existing costs of production held constant or close to constant. In these circumstances the model presented here has useful applications.

Constant Cost Industry Graph

In the constant cost industry graph below, we start with a typical representative firm and its average cost curve and marginal cost curve, which intersect at an output level of q and a price of p as illustrated. This is the profit maximizing price and output combination for this firm given current market circumstances.

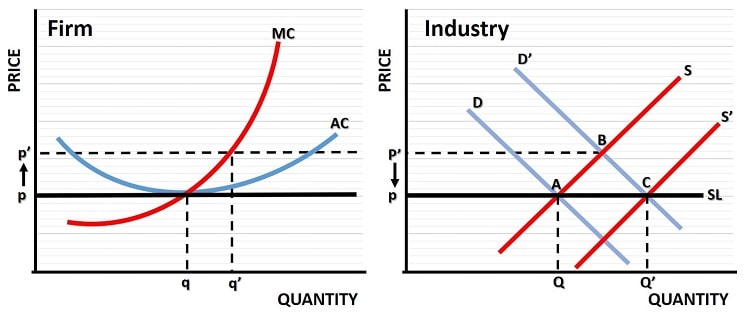
Now consider what happens if, for some reason, there is an increase in market demand for the product that this firm supplies. For example, suppose that the market under examination is the market for home treadmills. At the initial level of demand, the market is stable, but then a new body of research is made public that conclusively proves that jogging on treadmills 3 times per week will extend lifespan by 20 years!

Naturally, in light of this new research, there will be a significant increase in demand for treadmills. However, in the short-run firms can only increase production of treadmills via their existing facilities, which might mean paying overtime rates to existing workers, running night-shifts, weekend shifts, hiring new trainees and so on. This will no doubt come at an extra cost per unit of output which, combined with the increased demand, will push prices somewhat higher. This is illustrated on the left side of the diagram with an increase in output from q to q', and an increase in price from p to p'.

Other treadmill manufacturers will experience the same increase in costs per unit of output such that the whole industry sees prices rise to p'. On the right side of the constant cost industry graph, the increase in market demand that led to this price increase is illustrated with a move of the demand curve from D to D'. This results in a new intersection of demand curve and supply curve, with equilibrium moving from point A to point B as illustrated.

Now, since we know that firms can produce q output at a price of p, the increased price of p' will attract new entrants into the industry because of excessive economic profit, as well as spurring existing manufacturers to invest in more production facilities. In the long-run a full adjustment occurs via an expansion of the market supply curve from S to S' with a final intersection of demand and supply at point C.

Once equilibrium is reached at point C, the original price of p is restored, but industry output will have permanently expanded from Q to Q'. This is precisely what happens in a constant cost industry, and we can infer from this that the long run industry supply curve here is horizontal, as shown by the black line SL.

Costs are constant along the SL line because production facilities have had time to expand in order to meet the extra demand, and there are no limiting factors to inhibit that expansion. Similarly, there are no factors at play that can reduce costs via any sort of efficiencies of scale, so long run costs are more or less constant.

Real World Examples of Constant Cost Industries

Real world constant cost industry examples are limited, and in truth there are only approximations of this industry structure since most input costs are subject to some sort of scarcity, meaning that their prices will usually rise as their consumption is increased.

There is also a limiting factor in terms of industry structure, because only those industries that closely fit with the model of perfect competition will be able to expand production via the entry of new firms. Monopolistic and oligopolistic industry structures have significant barriers to entry that allow existing firms to restrict supply in order to extract higher profits from increasing prices.

With all these provisos in mind, the constant cost industry model does still have practical relevance for a great many competitive industries, especially where individual firms produce highly homogenized products. Many food products fit this description, as do many local retail services like hairdressers, bars & restaurants, clothing shops and so on.

Simple manufactured products like component parts often have constant cost structures, because competition to produce those parts is intense. When industries have branded products then supply is monopolized meaning that extra demand usually results in increased prices and profits for the brand in question.

Note however, that branded products can often be produced at a constant cost, it is only the sale of branded items that is limited to a single firm. These firms use their brand-power to extract higher prices from consumers, increasing their profit margins along the way, even though their costs are constant. This is one reason why recognized branding is so important.

On the other hand, firms will struggle to build brand recognition for free, and significant investment in advertising, provision of guarantees and warranties, quality assurance and customer care etc is usually required. If these extra costs are offset by gains from improved efficiency of scale, then costs may again be reasonably constant.

Conclusion - Long Run Adjustments

The constant cost industry model has value as an approximation of many competitive industries in the real world, but it is less useful where products are less homogenized and more specialized. Entry barriers that restrict new entrants into the industry will also prevent production increases from reaching optimal levels, and will therefore interfere with long run equilibrium price and output adjustments.

Since input costs will usually increase as an industry increases its quantity of output produced, the main alternative to the constant cost model is the 'increasing cost industry'.

It is also perfectly possible that some industries will experience falling costs as output levels expand, with economies of scale being the main driver of these falling costs. In this scenario, the 'decreasing cost industry' model is appropriate.

We should also note that as a typical industry evolves over time there may be significant changes to its cost structure due to technological advances. Cost adjustments driven by increasing levels of automation due to technological advances will affect the long-run industry supply curve. Accounting for these sorts of changes is difficult for any industry, because the long run is an unknown variable.

Related Pages:

• The Long Run Average Cost Curve
• The Production Possibilities Curve

ShareFacebookXPinterestTumblrRedditWhatsApp