Steve Bain

The Compensated Demand Function (Hicksian Demand)

A compensated demand function (also known as the Hicksian demand function) describes how the quantity demanded of a good changes as its price changes, holding the consumer's utility (or overall economic well-being) constant by adjusting income.

For example, if a good increases in price, it will increase the cost of living and reduce the consumer’s well-being, so Hicksian demand includes an increase in income to compensate for the higher cost of living. This is unlike the ordinary demand function (Marshallian demand), which considers how demand responds to price changes while taking a consumer’s income as a given.

The purpose of the compensated demand function is to isolate the substitution effect of a price change by removing the income effect. This is useful for understanding consumer behavior when utility is prioritized over actual income changes, and for a better understanding of this please refer to my articles about:

To reiterate: the ordinary demand function combines both substitution and income effects, while the compensated demand function accounts only for the substitution effect.

An Example of Hicksian Demand

Suppose the price of a good increases. Under ordinary demand consumers buy less due to both the good being relatively more expensive (substitution effect) and an effective reduction in the purchasing power (income effect) of a fixed income.

Compensated Demand Function Graph

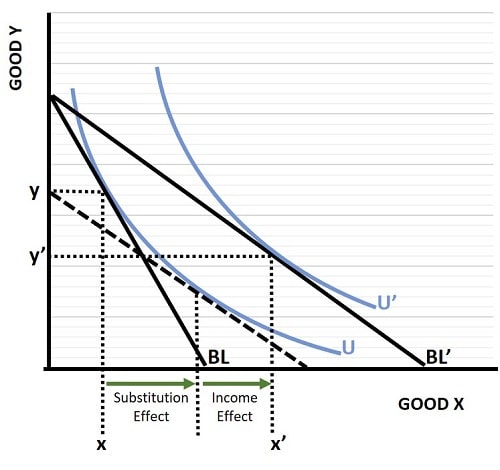
For illustrative purposes, the graph above is the one that I have presented in my articles about income and substitution effects. The budget line (BL) illustrates all the possible combinations of good x and good y that can be purchased with a fixed income. Now, after a reduction in the price of good x, a consumer can increase his/her economic well-being (utility) by moving from a consumption bundle of x, y to x’, y’ (with the increased utility illustrated by the upward shift of the blue indifference curve from U to U’ and a new budget line at BL’).

With Hicksian demand, income would be reduced to counter the increased utility resulting from a lower cost of living. This would imply a movement in consumption preferences along the original indifference curve, and the dashed line would be the new budget line. The consumer would choose to consume at the point where the dashed budget line just touches the original indifference curve, as that is the highest level of utility possible given the reduction in income. At that point, you can see in the graph that only the substitution effect is relevant, and that the income effect has been nullified.

This is the point, under compensated demand, the income is adjusted to compensate for the utility gain/loss, leaving only the substitution effect visible in the change in quantity demanded.

Practical Application of The Compensated Demand Function

In policy analysis, compensated demand is used to evaluate the effect of taxes or subsidies by focusing purely on how price changes influence choices, independent of income variations.

It is also central in calculating ‘consumer surplus’ or the compensating variation (the amount of money a consumer needs to reach the same utility after a price change).

FAQs about Hicksian Demand

What is the duality relationship between the Hicksian and Marshallian demand functions?

The Hicksian demand function is derived from the expenditure minimization problem, while the Marshallian demand is derived from the utility maximization problem. The two are duals because changes in one reflect changes in the other via the expenditure or utility function.

What is the significance of Slutsky's equation in the context of compensated demand?

Slutsky's equation decomposes the total effect of a price change into the substitution effect (compensated demand) and the income effect. This relationship helps in distinguishing the roles of these effects in shaping consumer behavior.

How does the compensated demand curve look compared to the ordinary demand curve?

The compensated demand curve is generally steeper than the ordinary demand curve because it accounts only for the substitution effect, ignoring changes in purchasing power caused by the income effect.

How does compensated demand relate to the concept of welfare economics?

Compensated demand is crucial for welfare analysis as it helps measure changes in consumer welfare through metrics like compensating variation and equivalent variation, which quantify monetary adjustments needed to maintain utility levels.

What role does the compensated demand function play in determining deadweight loss?

Compensated demand is used to calculate deadweight loss by isolating how price distortions (e.g., taxes) change consumer and producer behavior, independent of income effects, to quantify efficiency losses.

What assumptions underpin the compensated demand function?
  • Utility is measurable and constant.
  • Preferences are rational and transitive.
  • Consumers respond predictably to price changes (substitution effect dominates).
  • Income adjustments can perfectly offset changes in purchasing power.

How do compensated demand functions handle non-linear preferences?

Non-linear preferences, represented by curved indifference curves, can still be analyzed using compensated demand functions, but the resulting substitution effects are more complex due to varying marginal rates of substitution.

Related Pages:

Show / Hide