Utility Function (Graph, Formula & Example)

The Utility Function in Economics adds a degree of measurable, or comparable, analysis for the indifference curves that we use in modeling consumer behavior. The numbers ascribed to these functions are meaningless in themselves, but they can be used for comparison purposes.

For economists the word utility means a great deal, and much of microeconomics is built on the notion of marginal utility, i.e., the value of one more good, or one more input unit in the production process. Total utility pales in significance when compared to marginal utility when considering, for example, the market price of goods. The whole Diamond Water Paradox is explained via the way in which consumers value the marginal unit rather than good itself.

With a utility function, we can add an extra degree or two of usefulness to our overall model of consumer behavior. When a consumer purchases a good, the price paid is always worth less to the consumer than the expected utility that will be gained from that good, otherwise no purchase would be made.

The Utility Function Graph

If the utility function graph below looks familiar, that's because it is simply the indifference map that featured on my page about indifference curves. The only difference is that this time each curve has been graphed according to an arbitrary numerical value.

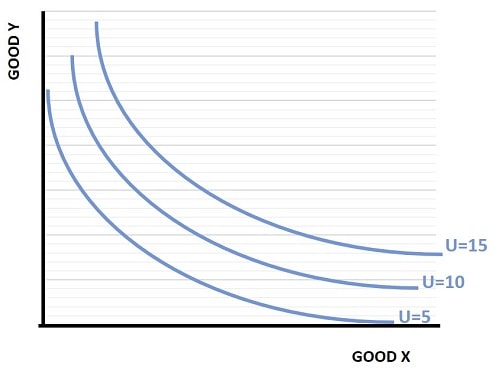
The numerical value relates to what economists call utils i.e., how much utility pertains to each indifference curve. If you have forgotten what these curves represent and need a refresher, have a look at my main article about:

• Indifference Curves and Maps

'Utils' cannot be bought or sold, they can't be traded, and they can't be transferred. That's because they don't exist in the real world, they are just an arbitrary concept that serve a single purpose, and that is to compare/rank different levels of utility gained from baskets of goods and services. Keep in mind that the term 'utility' in economics is used exclusively for this purpose - to assign a numerical value to one basket of goods & services compared to another.

A Utility Function Example

Sticking with the same two-good model that I have used on related pages, let's consider the utility gained from a basket of biscuits and cheese. By observing how consumers spend their money on these items at various prices it is possible to deduce their preference - it's a process called revealed preference.

From this we can construct typical utility functions to estimate the utility gained from different combinations of biscuits and cheese. Let's keep this example really simple:

Utility Function Formula

U(B,C) = B + 10C

In words this means that the utility from biscuits and cheese equals one multiplied by the servings of biscuits plus ten multiplied by the servings of cheese. So, if we have two baskets of these goods with different quantities of each good, we can compare the overall utility of each basket:

• Basket A has 5 servings of biscuits and 2 servings of cheese, yielding 25 utils.
• Basket B has 10 servings of biscuits and 1 serving of cheese, yielding 20 utils.

Two things should be noted here:

1. Basket A is preferred to Basket B because it gives more utility.
2. This is the important bit - whilst A is preferred, we cannot determine by how much!

Take good note of point 2 here, because the numbers assigned here are not comparable in a mathematical sense. In other words, we cannot say that 4 baskets of A would give 100 utils and that 5 baskets of B would also give 100 utils. Utils are not additive in this manner, they can only be used to rank one basket as preferred to another, they cannot be used to measure by how much one is preferred to another.

Different Utility Functions - Ordinal & Cardinal

The form of ranking different baskets of goods with individual utility functions has a specific name, it is referred to as ordinal ranking. We rank the order in which baskets are preferred, but we do not know by how much they are preferred.

Utility functions based on ordinal rankings are also specific to each consumer. If Jack gains 12 utils from a serving of cheese and Jane gains 10 utils, we cannot deduce that Jack gains more utility from cheese than Jane does. We only know that the 12 utils he gains are better for him personally than some other good that gives him 10 utils. In other words, a given number of utils for one person may represent an entirely different amount of utility than it represents for a different person.

The restrictions on what can be deduced from ordinal utility may seem severe, and may appear to render the whole concept somewhat useless. Certainly we would like to be able to quantify and compare exactly how much utility we gain from consuming goods, and if we could do this we would be able to construct 'cardinal utility functions'. However, we simply cannot tell exactly how much utility a consumer gains from consuming a good. Even the same consumer at a given time experiences diminishing marginal utility from additional units of the same good, so quantifying this over time, across different consumers, and for differing quantities is impossible.

Happily, cardinal utility functions are unnecessary. Ordinal utility is quite sufficient for us to be able to form useful models of consumer behavior.

Expected Utility for Different Goods

The expected utility from consuming goods varies depending on the type of goods being consumed. On this page (and on all others unless stated otherwise) I refer to 'normal goods' i.e., those for which the three assumptions underlying consumer behavior theory are satisfied. Those 3 assumptions relate to completeness, transitivity, and non-satiation. For more details on these assumptions, see my main article at:

• Consumer Behavior Theory

We should, however, keep in mind that there are many other types of goods. I'll be covering these in separate articles as I build up the microeconomics section of the site. See the related pages below for info.

Related Pages:

• Marginal Utility
• Marginal Rate of Substitution
• Budget Line & Budget Constraint
• Engel Curve
• Types of Economic Goods

ShareFacebookXPinterestTumblrRedditWhatsApp