- Home
- Market Failure
- Pigouvian Subsidy

Pigouvian Subsidy Definition & Examples
A Pigouvian subsidy (also called Pigovian subsidy after Arthur Cecil Pigou introduced the concept) is sometimes applied to those markets that have positive externalities attached to them. The idea is to encourage more production and consumption in order to reach a more efficient outcome that fully utilizes the potential gains that the free market will leave on the table.
A subsidy is just one of several options that a government could take in order to reach a more socially efficient quantity of production in the market, but it is usually one of the most effective options. Other options include marketing and promotion, or direct controls such as mandating extra production, or possibly even nationalizing the particular industry in order to provide the desired quantity of goods or services directly to the public.
A subsidy is usually the simplest and most efficient means of moving the free market to the desired equilibrium point, and a graph can easily illustrate how it works.
Pigouvian Subsidy Graph
Starting with the free market supply and demand curves in the graph below i.e., the red S=MPC and black MPB curves (where MPC means marginal private cost, and MPB means marginal private benefit), we can see that these intersect at a quantity of q and a price of p. However, the marginal private benefit curve (which is simply another name for the demand curve when there are externalities present) does not represent the full benefits to society.
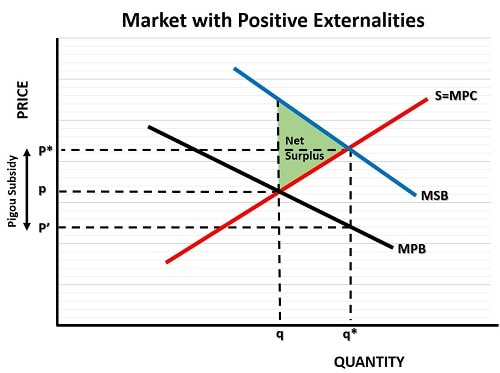
The full benefits are represented by the blue MSB curve (which stands for marginal social benefit), and the efficient equilibrium point in the market occurs at its intersection with the red supply curve S=MPC i.e.,where the marginal social benefit equals the marginal social cost.
As can be seen in the graph, this results in an efficient equilibrium price of p* at an efficient output level of q*, and the net gains to society from this are illustrated by the green area above the supply curve and below the MSB curve.
Why is this green area indicative of the extra gains to society? Because for each extra unit of output from the original level of q, up to the optimal level of q*, we can clearly see that the marginal social benefits are higher than the costs (represented by the red supply curve).
However, at an output rate of q*, the black marginal private benefit curve shows that private individuals will only pay a price of p', which means that a Pigouvian subsidy will need to pick up the shortfall, and be equal to p* - p'.
Pigouvian Subsidy Formula
From the graph above we can derive the Pigouvian subsidy formula that will yield the most surplus for society. The overall cost of the subsidy can be written as:
Cost = q*(p* - p')
Both producers and consumers will benefit, with an extra consumer surplus equal to the top part of the green area, and extra producer surplus equal to the bottom part of the green area.
Consumers clearly benefit because because the price that they pay has fallen whilst their consumption has increased. Firms also clearly benefit because the price that they receive has risen and their sales have increased.
Only the taxpayer loses out, because taxes will need to rise in order to pay for the subsidy. However, whilst the extra tax burden is not illustrated (because it gets complicated by the extra tax receipts generated from the businesses whose profits are now higher), the green area in the diagram does illustrate the overall net benefit after costs are accounted for.
Pigouvian Subsidy Examples
I have written about the most obvious examples of industries/products with positive external benefits on my page about externalities, so head over their via the link for details. As a reminder, here is a short list of examples:
- Public Goods - i.e. goods that have benefits for all users but whose benefits are non-excludable, meaning that if person A pays for it, it will be used by person B. National Defense, Highway Maintenance, the Police Service etc are all examples.
- Research & Development - R&D leads to all sorts of new discoveries and applications over and above those that were originally paid for by the business that funded the research.
- Vaccines - the most obvious example of all, because if person A gets a vaccine then person B will benefit because he/she will not be able to get infected by person A.
Of these examples, R&D and Vaccines are most suited to a Pigouvian subsidy. Public goods are, by definition, fully nationalized and provided directly by the state out of tax revenue, borrowing or money printing.
Pigovian Subsidy vs Tax
Pigouvian Tax Advantages
A Pigouvian Tax is a corrective tax that is levied (usually on the business but sometimes on the consumer) in order to reduce or eliminate an external cost that is borne by third parties. I have written about this on my page about:
These sorts of taxes are basically the opposite of a Pigouvian subsidy, and the advantages that they confer for society work with an identical logic to subsidies but in the opposite direction. By placing a Pigouvian tax on a product that creates a cost for third parties, it influences firms to reduce the output level of that product to a more efficient equilibrium point.
Questions & Answers
- What is the optimal Pigouvian Subsidy?
The Optimal subsidy, as with taxes, depends on which beneficiary we are referring to. The correct frame of reference is to answer this question with a view to the overall societal benefit, and in this case the optimal subsidy for government to pay is given by the formula above i.e., q*(p* - p'). However, if we are talking about a business or consumer who is the recipient of that subsidy, then clearly the more the better...
- How do you get a Pigouvian Subsidy?
Whilst it is possible for a government to automatically subsidize or tax an industry for the purpose of correcting an external cost (or boosting an external benefit) the usual application of such a policy comes about after significant lobbying by interest groups. For a business that enter an industry which already has an existing tax/subsidy policy in place, accessing it may require an application to a managing body, or via the government tax office.
- What about the long run cost & efficiency?
The common problem with all Pigouvian interventions in the market, whether via a tax or a subsidy, is that it is extremely difficult to know the exact positions of all these marginal curves. The implication is that we don't know what level of tax will be needed to fund a subsidy, or what amount of tax should be imposed, to reach the optimal solution. Even if we had a reasonable idea of these curves at a given point in time, these things are not fixed. Circumstances change over time and a good Pigouvian policy one year might be bad the next. This will inevitably incur inefficiency, and there is a risk that the cost of these policies might become excessive.
Sources:
Related Pages: